Why the proof of closure under addition in Linear Map is $(T+S)(u+

I am reading Linear Algebra Done Right and want to prove that $L(V, W)$ is a vector space. I have read the solution here: Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ inst

Solved 2. Prove that there exists a linear transformation T

Math Properties, Commutative, Associative & Distributive - Lesson

FCLA Injective Linear Transformations

solution verification - Proving the existence of a linear map such that a function diagram is commutative - Mathematics Stack Exchange

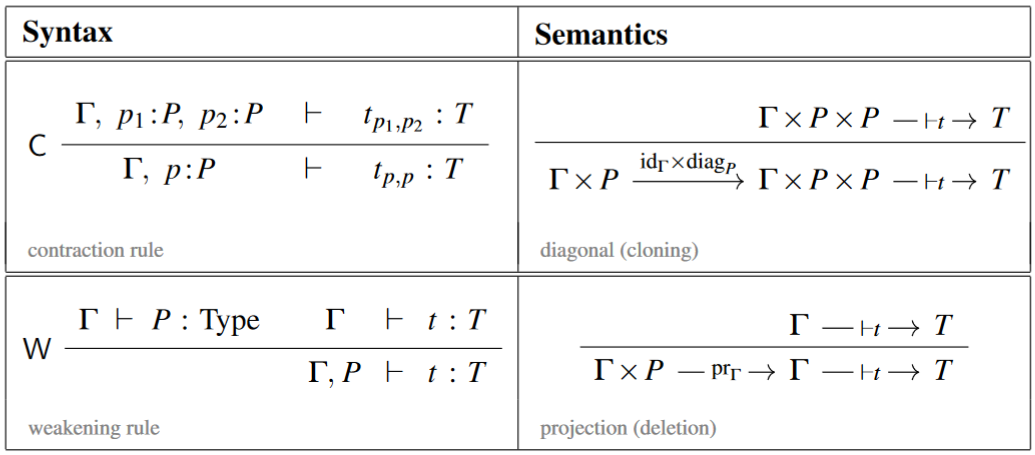
linear logic in nLab

Linear subspace - Wikipedia

What does 'Vectors are closed under addition' mean? - Quora

Sensors, Free Full-Text

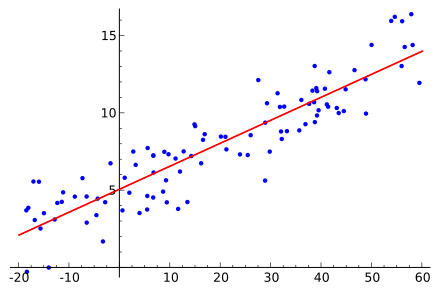
Closed-Form Solution to Linear Regression, by Margo Hatcher

Determinant - Wikipedia

Solved Let T:R2→R2 be a linear transformation that maps

Velocity-addition formula - Wikipedia

Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ instead of $(T+S)(u)$ and $(T)(u+v)$? - Mathematics Stack Exchange

Orthogonal Set of Vector - an overview